Quantum-inspired Processing for System Optimization in Emerging Networks
Dilip Krishnaswamy (This email address is being protected from spambots. You need JavaScript enabled to view it.)
Abstract
This paper explores quantum-inspired techniques for resource management and optimization of emerging wireless networks. As wireless networks continue to evolve into 6G and beyond, the deployment of networks will be increasingly heterogeneous comprising of base-stations or access points or distributed units serving users in different spectra utilizing different technologies, with self-organizing features enabled. A Quasi-quantum graph colouring algorithm can be considered using virtual cell identifiers to coordinate across access nodes and to enable such networks to be optimized. Dynamic energy savings can be performed in a quadratic unconstrained binary optimization framework. Dynamic load balancing is suggested using an entangled quantum state variable across access nodes, to represent a distributed network availability state. In general, a distributed probabilistic quantum state vector can be utilized to enable quantum-inspired resource optimization in emerging networks for different network optimization problems.
Introduction
As research in the 6G domain advances, the telecommunications industry is entering an inflection point to pursue interesting challenges to work on newer network architecture paradigms and to utilize new and emerging technologies. The increased heterogeneity of technologies for accessing networks such as based on 4G or 5G-NR or WiFi6 or 5G-NR-Unlicensed or B5G (Beyond 5G) or 6G [1][2][3][4], variability in large and small cells, options for centralized versus disaggregated RAN (Radio Access Network) solutions, and programmable infrastructure, ensuring different levels of quality of service for different network slices, distributed and partitioned private and public 5G and edge networks, smart utilization of local and distributed intelligence in networks, and enabling new applications and services, all provide interesting challenges for system optimization in such networks. Such emerging systems will process information in an increasingly distributed and probabilistic manner. This paper provides a framework to explore quantum-based processing to help with system optimization in such emerging networks.
RAN System Optimization
To optimize resources in the RAN domain, the O-RAN (Open RAN) architecture [5] includes capabilities for a Non-Real-Time RAN Intelligent Controller (NonRT-RIC) in a Service and Management Orchestration (SMO) layer associated with the RAN to assist with delay-tolerant optimizations for the RAN. In addition, a Near-Real-Time RAN Intelligent Controller (NearRT-RIC) is placed closer to the RAN to assist with delay-sensitive optimizations for the RAN. These RICs interact with Central Units (CUs), or Distributed Units (DUs) or Radio Units (RUs) in the network. The RU provides support for antennas, radio communications (Tx/Rx), and the lower physical layer. The DU provides support for lower layers of the overall RAN protocol stack such as the upper physical layer, the MAC layer and the RLC layer. The CU provides support for control and upper layers of the RAN protocol stack such as the RRC, PDCP, and the SDAP layers. System information metrics/parameters from the CUs, DUs, and RUs are monitored and aggregated at the RICs and stored in a system information model (typically a yang model) that can vary dynamically. Changes to such a system model are continuously monitored. In addition, changes to specific metrics that are related to a specific optimization function can be computed and monitored, and these changes can be used to trigger the execution of such optimization functions. These optimization functions can relate to Self-Organizing Network (SON) [6][7][8] functions for the RAN and into other network segments which have been progressively proposed in cellular standards including
- Automatic Neighbor Relations (ANR)
- Automatic Physical Cell ID (PCI) assignment
- Mobility Robustness/Handover optimization (MRO)
- Load Balancing Optimization (LBO)
- Coverage & Capacity Optimization (CCO)
- Random Access Channel (RACH) Optimization
- InterCell Interference Coordination (ICIC)
- Enhanced InterCell Interference Coordination (eICIC)
- Minimization of Drive Testing (MDT)
- Energy Savings (ES)
- Handover Optimization (HO)
- Cell Outage Detection and Compensation
- Self-healing Functions
- Coordination between various SON Functions
Typically, most SON functions are processed in a centralized manner. A more flexible realization for Hybrid SON is also possible that utilizes both distributed SON and centralized SON, allowing the distributed optimization components to focus on local optimization, whereas the centralized SON optimizes across the distributed components, providing useful feedback to the distributed components for improved local optimization.
In general, a Heterogeneous RIC (Het-RIC) [18] can be explored, where such a Het-RIC manages other radio access technologies and systems as well such as WiFi access points (APs), 4G eNodeBs, 5G gNodeBs, or 6G-cells, in addition to disaggregated components such as CUs, DUs, and RUs.
Quantum-Inspired Optimization
Quantum-based systems support the notion of a probabilistic state vector across different state dimensions in a system [9][10][11][12][13][18][20]. For emerging distributed processing systems in networks, quantum-state vectors can be used to represent the overall distributed state information in the system. The state of the system can then evolve probabilistically based on unitary transforms associated with quantum state variables. The amplitudes associated with quantum states can be progressively refined such that a collapse of the state can result in an optimal solution to a system optimization problem. Such an approach can be utilized for different types of system optimization problems such as PCI optimization in heterogeneous and disaggregated networks, distributed energy management in networks, load balancing in heterogeneous networks, or network-access coordination across access nodes and devices. A Quantum State Variable (QSV) can be associated with one or more physical qubits, or one or more virtual qubits. Quasi-quantum processing can be done using virtual qubits or quantum state variables (QSVs) in a classical computer. Alternatively, quantum processing can be done using physical qubits in a quantum computer. Hybrid implementations are also possible where some processing is done in a quantum computer assisted by processing performed on a classical computer. In the case of a physical qubit, the state of the qubit will not be fixed and will remain in a state of superposition, until it is measured. Prior to measurement, a physical qubit is in a state of superposition across possible states. When the state of a physical qubit is measured, then the state of the qubit will collapse to one of the possible states.
Dynamic PCI Optimization
Traditionally, PCI optimization is formulated as an NP-complete graph coloring-based optimization problem with each cell as a node in the graph, with edges in the graph between neighboring cells [14][15][16][17][18]. To be relevant to emerging heterogeneous networks operating in virtualized infrastructure, one can create a virtualPCI (vPCI) number [18] that is managed in such infrastructure and associated with the cells, such that an extended range beyond [0-1007] is possible in the network. Cell IDs associated with non-4G or non-5G-NR cells or newer-6G cells could take on values beyond the available range for 4G/5G deployments. The color (equivalently the vPCI value) of a node i can take on one of any of 1≤k ≤ K colors in a network graph. The system optimization results in the determination of the value for the color of each of the cells such that PCI collision or confusion is avoided in the network. Dynamic optimization can be done locally utilizing only a small subset of IDs allocated to a network graph representing nodes in a local geographical region to avoid conflicts across regions. A collision occurs when two nodes have the same color or vPCI value in the same network graph. A confusion occurs when two neighbors of the same node have the same color or vPCI value in the network. From the perspective of a quantum-inspired framework, it would be useful to study this problem as a graph with nodes whose colors (PCI values) are determined based on a quantum-state variable (QSVs) associated with that node, where different states correspond to different possible color assignments to nodes. The state probabilities associated with the QSVs for the nodes in the graph can be refined when there are edge conflicts between nodes that have the same color. For this purpose, one can define a single Quantum State Variable (QSV)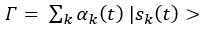 ………………………….…..(1)
………………………….…..(1)
with K states (or colors) that could be associated with a given cell, such that a collapse of the QSV to one of the K states results in the determination of the color (or vPCI value) for that cell [18]. The state of a QSV is given by a superposition of K states from the set {|s_1 (t)>, |s_2 (t)>, ……., |s_K (t)>}, such that |α_k (t) |^2 is the probability associated with state |s_K (t)>. The collisions in the graph are determined based on color conflicts given an adjacency matrix A for the network graph. Figure 1 shows the reduction in PCI conflicts as the optimization is iteratively performed. As the number of available colors was increased, the system required fewer iterations to converge as expected to eliminate conflicts, due to the greater degrees of freedom afforded by a larger number of available colors.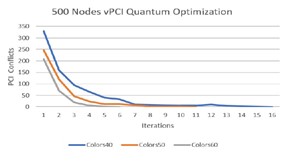
Figure 1: Quantum-inspired vPCI Optimization [18]
To avoid confusions in the network, a similar optimization is performed on the square of the adjacency graph A2 to determine two step-walks in the graph. This allows neighbors of a given node in a network graph with adjacency matrix A, to become neighbors of each other in a network graph with adjacency matrix A2. In effect, the detection of confusion in the original network graph with adjacency matrix A becomes equivalent to the detection of collision in the new network graph with adjacency matrix A2.
Dynamic Energy Savings
When the utilization of the network falls below a threshold such that the available capacity is large in different cells in the network, and if the corresponding access nodes (gNodeBs, eNodeBs, or WiFi-APs, or Distributed Units (DUs) associated with gNodeBs or 6G-cells) are jointly covering the same geographical region, then a D-Wave based quantum optimization framework can be relevant to determine which nodes to keep active, and which to turn off for energy savings. A D-Wave system [19] contains a Quantum Processing Unit (QPU) operated at a temperature close to absolute zero, where the system is designed to naturally execute annealing algorithms that attempt to minimize system energy. A D-Wave QUBO (Quadratic Unconstrained Binary Optimization) problem is defined with the goal of minimizing an energy function E (also known as the Hamiltonian for the system) given by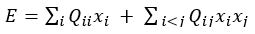 …………...…………..(2)
…………...…………..(2)
The terms x_i take on values 1 or 0 to indicate whether an access node is on or off in the system. This is based on the Ising Model where the variables represent "spin up" or "spin down" states. Self-coupling coefficients Q_ii can be used to provide an opportunity for a node to provide service with the value depending on the size of the coverage area provided by the node in the region. The more negative value of a self-coupling coefficient, the more likely that the node represented by the coefficient is turned on in the network. The cross-coupling coefficients Q_ij represent the degree of correlation between nodes in the network. Such a self-coupling coefficient can be used to provide an opportunity for a node to provide service where the value can depend on the size of the coverage area provided by the node in the region, or the cost of service from the node in the region. The coupling between two nodes can represent either a positive or negative correlation. A negative value of a cross-coupling coefficient increases the likelihood of two nodes jointly serving a network thus lowering energy in the system, whereas a positive value of the cross-coupling coefficients has the opposite effect, increasing system energy and reducing the likelihood of two nodes jointly serving the network. A positive value of the cross-coupling coefficient can be used for example, if two nodes have a common area that they are covering, so that the magnitude of the coupling reflects the degree of overlap. Similarly, a negative value could be used if two nodes cover different areas, with a higher degree of negative coupling if the nodes are highly separated from each other. If the cross-coupling coefficient Q_ij between two nodes has a positive value, and yet, if that cost is lower in magnitude relative to the magnitude of the sum of the negative self-coupling costs Q_ii and Q_jj for the two nodes i and j respectively, then the overall cost/energy to jointly utilize both access nodes is negative. Alternatively, if a positive cross-coupling coefficient is higher in magnitude relative to the negative self-coupling costs for the nodes, then the joint utilization of the nodes results in a higher energy system. In general, the costs associated with utilization of all access nodes needs to be jointly considered, so that a joint optimization across all nodes is needed for an overall determination of which access nodes can be kept on at any given time. This technique was implemented in the D-Wave QUBO simulator. For example, when the self-coupling values and cross-coupling values as listed in Table 1 are utilized, and the cross-coupling terms are utilized only once for any pair of nodes as shown in equation 2, then the system settles down to a low energy state of -14 units with an allocation of 10011 across the nodes, enabling nodes 1 and 2 to go to sleep, while keeping nodes 0, 3 and 4 active in the system. Such a formulation can thus be used for energy optimization across a network of base-stations or access points, by utilizing a quantum-system representing the system state to evolve, anneal, and settle down to a low energy state that minimizes system energy.
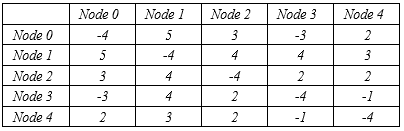
Table 1: Self-coupling and cross-coupling coefficients between access nodes for joint energy optimization in a network.
Dynamic Load Balancing Optimization
Consider N access nodes in a wireless network collaborating to provide access to different users in a network in a common geographical area. These nodes could be operating in different frequency bands in the same geographical region so that the load on access nodes is utilized to determine which node provides access to a particular user in that region. In that regard, one can create a QSV that is entangled across different access nodes in the network, where each access node has a state | si(t)> where i = 1, 2,…., N. Let us assume that we are seeking an access node i that can provide network access to a new user. In this regard, we can create a quantum state ψi(t) which is a superposition of the states |si(t)> for these N access nodes, where the state |si(t)> represents node i serving a new user at time t, given by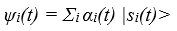 …………………….……………(3)
…………………….……………(3)
Here, the state probability is given by the square of the amplitude αi(t) representing the likelihood of access node i serving a new user at time t. In the simple case, when all states are equally likely with probability 1/N, then the amplitudes αi(t) have values 1/√N. In general, these probabilities across the access nodes would vary dynamically depending on the available capacity and current load at each access node. We seek an access node that has a lighter load relative to other nodes such that a node with a lighter load has a higher amplitude in the QSV, so that it would have a higher likelihood of being selected to serve a new user in the network. Since the nodes share an entangled QSV, a collapse of the QSV helps in determining which node provides access across all the nodes. To maintain an updated version of the state, each access node i would have to periodically exchange its current load Li(t) and their total capacity Ci(t), with other nodes in the network, to enable its dynamic available capacity, Ai (t) = Ci(t) – Li(t) to be computed by other nodes. Alternatively, nodes could merely exchange their dynamic available capacity Ai (t) periodically. This allows the state probabilities p_i(t) = A_i(t) / (Sigma_j A_j(t) ) to be computed so that they are proportional to the dynamic available capacities of each of the nodes i, to then determine the state amplitudes α_i (t)= √(p_i (t)) for the distributed probabilistic quantum state vector across the nodes. Such processing can be directly performed by a central neutral entity such as a Het-RIC associated with a heterogeneous Central Unit (Het-CU) that coordinates network access across the access nodes and performs a state collapse of an entangled QSV across the nodes. A quantum blockchain network [20] across these nodes can also be utilized, if desired, for shared distributed processing, to exchange and share metrics with a smart contract executed across nodes for shared decision-making. It can be seen from Figure 2 that the load gets progressively better-balanced across the network as new users join the network by utilizing the collapse of a QSV across the nodes to admit such new users. 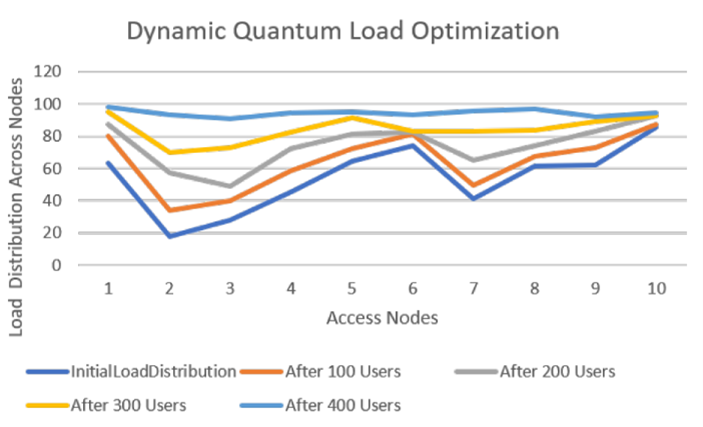
Figure 2: Dynamic Quantum Load Optimization across N access nodes (N = 10) serving mobile users in a wireless network
Each curve shows the distribution of load across the nodes after each iteration starting with the lowermost initial load distribution curve in the graph. As new users join the network, the load across the network is progressively distributed more equitably across the access nodes in the network.
Summary and Future Possibilities
To summarize, this paper has suggested quantum-inspired algorithms that utilize probabilistic state information in quantum state variables (QSVs), or entangled QSVs to assist with resource optimization in emerging wireless networks. Of late, RAN Intelligent Controllers are being explored in emerging programmable networks that operate across multiple cells and across available licensed/unlicensed wireless networks, that interact with centralized units (CUs) and/or distributed units (DUs) and/or WiFi Access points, where the suggested algorithms could be deployed. Resource management problems such as PCI optimization, energy optimization, and load balancing optimization were explored in this work. It is possible that other SON functions and system optimization problems could be explored in a similar manner utilizing the notion of a distributed probabilistic state that can be encapsulated in a quantum state variable.
References
[1] C. Johnson, “5G New Radio in Bullets,” 1st edition, 2019.
[2] IEEE 802.11 standards, https://www.ieee802.org/11/ [Online: Accessed January 15, 2022].
[3] IEEE Future Networks, “IEEE 5G and Beyond Technology Roadmap,” https://futurenetworks.ieee.org/images/files/pdf/ieee-5g-roadmap-white-paper.pdf [Online: Accessed January 15, 2022].
[4] 5G Infra Assoc, “European Vision for the 6G Network Ecosystem,”
https://5g-ppp.eu/wp-content/uploads/2021/06/WhitePaper-6G-Europe.pdf [Online: Accessed January 15, 2022].
[5] O-RAN Alliance, https://www.o-ran.org/ [Online: Accessed January 15, 2022].
[6] A. Chaub et al, “Self-Organizing Networks in the 6G Era: State of the Art, Opportunities, Challenges, and Future Trends,” https://arxiv.org/abs/2112.09769, [Online: Accessed January 15, 2022].
[7] N. Marchetti et al, “Self-Organizing Networks: State-of-the-art, challenges and perspectives,” Proc. IEEE Int. Conf. Commun. Workshops (ICC), June 2010.
[8] J. Moysen and L. Giupponi, “From 4G to 5G: Self-organized Network Management meets Machine Learning,” Computer Communications, Vol. 129, pp. 248-268. Sep 2018.
[9] R. Eisberg, and R. Resnick, “Quantum Physics of Atoms, Molecules,
Solids, Nuclei, and Particles,” 2nd edition, 2003, Wiley Publishing.
[10] B. H. Bransden and C. J. Jochain, “Quantum Mechanics,” 2nd edition, 2000, Pearson Education.
[11] M. A. Neilsen and I. L. Chuang, “Quantum Computation and Quantum Information,” 10th edition, Pearson Education, 2016.
[12] National Academies of Sciences, Engineering, and Medicine 2019, “Quantum Computing: Progress and Prospects,” Washington, DC: The
National Academies Press, https://doi.org/10.17226/25196. [Online: Accessed January 15, 2022].
[13] S. Imre, “Quantum Communications: Explained for Communication Engineers,” IEEE Communications Magazine, August 2013.
[14] M. Amirijoo et al, “Neighbor Cell Relation List and Physical Cell
Identity Self-Organization in LTE,” Proc. IEEE Int. Conf. Commun.
Workshops (ICC), May 2008, pp. 37–41.
[15] R. Acedo-Hernandez et al, “A PCI planning algorithm for jointly
reducing reference signal collisions in LTE uplink and downlink,”
Computer Networks, vol. 119, pp. 112–123, Jun. 2017.
[16] S. Nyberg, “Physical Celll ID Allocation in Cellular Networks,” Technical Report, Master’s Thesis, Linkoping University, 2016.
[17] J. Gui, Z, Jiang, S. Gao, “PCI Planning based on Binary Quadratic
Programming in LTE/LTE-A Networks,”, IEEE Access, vol 7, pp. 203-
214, 2019.
[18] D. Krishnaswamy, “Quasi-Quantum PCI Optimization in 5G Networks,” IEEE Vehicular Technology Conference, Spring 2021.
[19] D-Wave Systems, https://www.dwavesys.com/ [Online: Accessed January 15, 2022],
[20] D. Krishnaswamy, “Quantum Blockchain Networks,” BlockNet Workshop at ACM Mobihoc 2020.
Bio Dilip Krishnaswamy received a PhD in electrical engineering from the University of Illinois at Urbana-Champaign. He is an inventor on 60+ granted US patents, and has co-authored 70+ research publications. He has worked at Intel Corp., Qualcomm Research, IBM Research, and Jio Platforms, and he is currently a senior principal architect at Sterlite Access Solutions.
Dilip Krishnaswamy received a PhD in electrical engineering from the University of Illinois at Urbana-Champaign. He is an inventor on 60+ granted US patents, and has co-authored 70+ research publications. He has worked at Intel Corp., Qualcomm Research, IBM Research, and Jio Platforms, and he is currently a senior principal architect at Sterlite Access Solutions.
Subscribe to Tech Focus
Join our IEEE Future Networks Technical Community and receive IEEE Future NetworksTech Focus delivered to your email.
Article Contributions Welcome
Submit Manuscript via Track Chair
Author guidelines can be found here.
Other Future Networks Publications
IEEE Future Networks Tech Focus Editorial Board
Rod Waterhouse, Editor-in-Chief
Mithun Mukherjee, Managing Editor
Imran Shafique Ansari
Anwer Al-Dulaimi
Stefano Buzzi
Yunlong Cai
Zhi Ning Chen
Panagiotis Demestichas
Ashutosh Dutta
Yang Hao
Gerry Hayes
Chih-Lin I
James Irvine
Meng Lu
Amine Maaref
Thas Nirmalathas
Sen Wang
Shugong Xu
Haijun Zhang
Glaucio Haroldo Silva de Carvalho

